
Programa de Pós-graduação em Computação Aplicada – PPCA (UnB)
Análise Estatística de Dados e Informações
Professor: João Gabriel de Moraes Souza
Aluno: Angelo Donizete Buso Júnior
Índice ¶
- Compreensão Problema de Negócio
- 1.1. Dicionário dados
- Coleta Dados
- 2.1. Carga dados
- Análise Exploratória
- 3.1. Visão Geral dos dados
- 3.1.1. Variáveis Explanatórias e Variável Dependente
- 3.1.2. Missing Values
- 3.1.3. Análise Variável Dependente
- 3.1.3.1. Amplitude
- 3.1.3.2. Plot - boxplot
- 3.1.3.3. Plots Variável Dependente
- 3.1.3.4. Distribuição Dados - skw/Kurt
- 3.1.3.5. Relações Variável Dependente
- 3.1.4. Análise da Variáveis Explanatórias
- 3.1.4.1. Classificação das variáveis por tipo de dados
- 3.1.4.2. Explanatórias Numéricas
- 3.1.4.2.1. Plot - scatterplots
- 3.1.4.2.2. Correlação Atributos
- 3.1.4.2.3. Plot - Matriz de Correlação
- 3.1.4.2.4. Avaliando a Multicolinearidade
- 3.1.4.3. Explanatórias Categóricas
- 3.1. Visão Geral dos dados
- Pré-Processamento Dados
- 4.1. Feature Engineer
- 4.1.1. Dummies
- 4.1.2. Imputação Missing
- 4.2. Split Dados
- 4.2.1. Estático - nível linha
- 4.1. Feature Engineer
- Seleção Algoritmo
- 5.1. Algoritmos Regressores
- 5.1.1. Regressão Linear
- 5.2. Performance para Regressores
- 5.3. Distribuição dos resíduos
- 5.1. Algoritmos Regressores
- Conclusões
- Bibliografia
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.api as sm
from scipy.stats import kurtosis, skew
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
1. Compreensão Problema de Negócio ¶
O mercado imobiliário é um dos setores mais dinâmicos e competitivos da economia, demandando análises precisas e modelos robustos para avaliar o impacto de diferentes características no preço de venda de propriedades. Neste trabalho, atuamos como analistas de dados imobiliários para explorar, modelar e interpretar os fatores que influenciam os preços de propriedades em Ames, Iowa, utilizando técnicas de regressão linear como ferramenta principal. O objetivo é construir insights relevantes e práticos para a tomada de decisão no mercado imobiliário.
Para garantir a estruturação e a organização das etapas do projeto, adotamos a metodologia CRISP-DM (Cross-Industry Standard Process for Data Mining). Este framework é amplamente utilizado em projetos de ciência de dados e fornece um guia robusto que abrange desde a compreensão do problema de negócio até a avaliação e implementação do modelo. A metodologia garante que cada etapa seja bem definida e alinhada ao objetivo final. Segundo Shearer (2000), o CRISP-DM é "um modelo de processo não proprietário que descreve abordagens comuns usadas por especialistas para resolver problemas de mineração de dados."
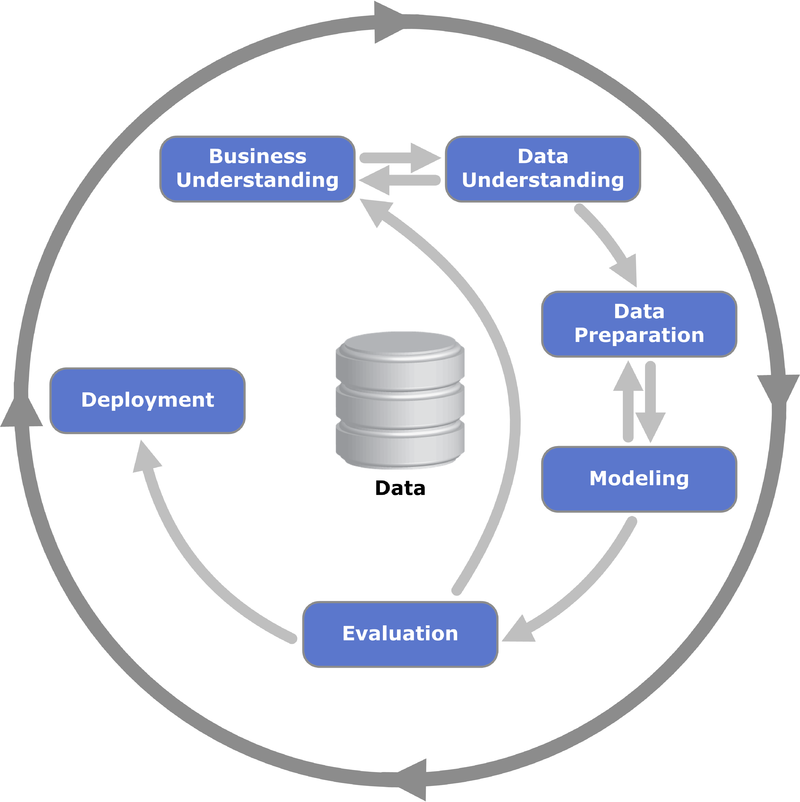
Abaixo está o framework CRISP-DM, composto por seis etapas principais:
Compreensão do Problema de Negócio: Definir os objetivos e requisitos.
Compreensão dos Dados: Coletar, descrever e explorar o conjunto de dados.
Preparação dos Dados: Limpar, transformar e selecionar as variáveis relevantes.
Modelagem: Escolher a técnica de modelagem, ajustar e avaliar os modelos.
Avaliação: Verificar se os modelos atendem aos objetivos definidos.
Implementação: Integrar os resultados para gerar valor ao negócio.
from IPython.display import Image
Image(url="https://upload.wikimedia.org/wikipedia/commons/thumb/b/b9/CRISP-DM_Process_Diagram.png/800px-CRISP-DM_Process_Diagram.png")
Neste trabalho, utilizamos o Ames Housing Dataset, disponível em Kaggle, que contém informações sobre 2930 propriedades na cidade de Ames, Iowa. As variáveis incluem características como número de quartos, área do terreno, presença de garagem, lareira, piscina, entre outros. Esses dados oferecem uma oportunidade única de explorar como diferentes atributos influenciam o preço de venda das propriedades.
Além disso, esta análise buscará evidenciar os pressupostos da regressão linear, utilizando testes estatísticos e visualizações para garantir a robustez dos resultados.
Portanto, este trabalho não apenas busca construir um modelo preditivo, mas também fornecer insights interpretáveis sobre o impacto de características imobiliárias no preço de venda. Podendo ainda ao final, o leitor encontrar o quão grande pode ser um trabalho de machine learning e ciências de dados pos nem sempre, nos primeiros ensaios, chega-se a um modelo definitivo!
1.1 Dicionário dados ¶
Abaixo transcrevemos o significado de cada um dos colunas do dataset.
- 1st Flr SF Área do primeiro andar em pés quadrados
- 2nd Flr SF Área do segundo andar em pés quadrados
- 3Ssn Porch Área da varanda de três estações em pés quadrados
- Alley Tipo de acesso ao beco
- Bedroom Número de quartos acima do solo
- Bldg Type Tipo de habitação
- Bsmt Cond Avaliação da condição geral do porão
- Bsmt Exposure Refere-se a paredes de nível de jardim ou walkout
- Bsmt Full Bath Número de banheiros completos no porão
- Bsmt Half Bath Número de meios banheiros no porão
- Bsmt Qual Avaliação da altura do porão
- Bsmt Unf SF Área não acabada do porão em pés quadrados
- BsmtFin SF 1 Tipo 1 de área acabada em pés quadrados
- BsmtFin SF 2 Tipo 2 de área acabada em pés quadrados
- BsmtFin Type 1 Avaliação da área acabada do porão
- BsmtFinType 2 Avaliação da área acabada do porão (se houver vários tipos)
- Central Air Ar condicionado central
- Condition 1 Proximidade a várias condições
- Condition 2 Proximidade a várias condições (se mais de uma estiver presente)
- Electrical Sistema elétrico
- Enclosed Porch Área da varanda fechada em pés quadrados
- Exter Cond Avaliação da condição atual do material no exterior
- Exter Qual Avaliação da qualidade do material no exterior
- Exterior 1 Revestimento exterior da casa
- Exterior 2 Revestimento exterior da casa (se mais de um material)
- Fence Qualidade da cerca
- Fireplace Qu Qualidade da lareira
- Fireplaces Número de lareiras
- Foundation Tipo de fundação
- Full Bath Número de banheiros completos acima do solo
- Functional Classificação da funcionalidade da casa
- Garage Area Área da garagem em pés quadrados
- Garage Cars Tamanho da garagem em termos de capacidade de carros
- Garage Cond Condição da garagem
- Garage Finish Acabamento interior da garagem
- Garage Qual Qualidade da garagem
- Garage Type Localização da garagem
- Garage Yr Blt Ano de construção da garagem
- Gr Liv Area Área total de convivência acima do solo em pés quadrados
- Half Bath Número de meios banheiros acima do solo
- Heating QC Qualidade e condição do aquecimento
- Heating Tipo de aquecimento
- House Style Estilo da habitação
- Kitchen Qual Qualidade da cozinha
- Kitchen Número de cozinhas
- Land Contour Planicidade da propriedade
- Land Slope Inclinação da propriedade
- Lot Area Tamanho do lote em pés quadrados
- Lot Config Configuração do lote
- Lot Frontage Metros lineares de rua conectados à propriedade
- Lot Shape Forma geral da propriedade
- Low Qual Fin SFÁrea de acabamento de baixa qualidade em pés quadrados
- Mas Vnr Area Área de revestimento de alvenaria em pés quadrados
- Mas Vnr Type Tipo de revestimento de alvenaria
- Misc Feature Outras características diversas
- Misc Val Valor de outras características diversas
- Mo Sold Mês de venda
- MS SubClass Tipo de habitação envolvida na venda
- MS Zoning Classificação geral de zoneamento da venda
- Neighborhood Localizações físicas dentro dos limites da cidade de Ames
- Open Porch SF Área da varanda aberta em pés quadrados
- Order Número de observação
- Overall Cond Avaliação da condição geral da casa
- Overall Qual Avaliação da qualidade geral do material e acabamento da casa
- Paved Drive Tipo de entrada pavimentada
- PID Número de identificação do lote
- Pool Area Área da piscina em pés quadrados
- Pool QC Qualidade da piscina
- Roof Matl Material do telhado
- Roof Style Tipo de telhado
- Sale Condition Condição da venda
- Sale Type Tipo de venda
- Screen Porch Área da varanda com tela em pés quadrados
- Street Tipo de acesso rodoviário à propriedade
- Total Bsmt SF Área total do porão em pés quadrados
- TotRms AbvGrd Número total de quartos acima do solo (excluindo banheiros)
- Utilities Tipo de utilidades disponíveis
- Wood Deck SF Área do deck de madeira em pés quadrados
- Year Built Data de construção original
- Year Remod/Add Data de reforma (mesma que a data de construção se não houver reformas ou adições)
- Yr Sold Ano de venda
path = "/home/wsl/projetos/mestrado/AEDI/dados/AmesHousing.csv"
data = pd.read_csv(path)
data.head()
| Order | PID | MS SubClass | MS Zoning | Lot Frontage | Lot Area | Street | Alley | Lot Shape | Land Contour | ... | Pool Area | Pool QC | Fence | Misc Feature | Misc Val | Mo Sold | Yr Sold | Sale Type | Sale Condition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 526301100 | 20 | RL | 141.0 | 31770 | Pave | NaN | IR1 | Lvl | ... | 0 | NaN | NaN | NaN | 0 | 5 | 2010 | WD | Normal | 215000 |
| 1 | 2 | 526350040 | 20 | RH | 80.0 | 11622 | Pave | NaN | Reg | Lvl | ... | 0 | NaN | MnPrv | NaN | 0 | 6 | 2010 | WD | Normal | 105000 |
| 2 | 3 | 526351010 | 20 | RL | 81.0 | 14267 | Pave | NaN | IR1 | Lvl | ... | 0 | NaN | NaN | Gar2 | 12500 | 6 | 2010 | WD | Normal | 172000 |
| 3 | 4 | 526353030 | 20 | RL | 93.0 | 11160 | Pave | NaN | Reg | Lvl | ... | 0 | NaN | NaN | NaN | 0 | 4 | 2010 | WD | Normal | 244000 |
| 4 | 5 | 527105010 | 60 | RL | 74.0 | 13830 | Pave | NaN | IR1 | Lvl | ... | 0 | NaN | MnPrv | NaN | 0 | 3 | 2010 | WD | Normal | 189900 |
5 rows × 82 columns
3. Análise Exploratória ¶
3.1 Visão Geral dos dados ¶
A análise exploratória de dados (EDA) é um passo essencial em projetos de ciência de dados, pois permite uma melhor compreensão das características, distribuições e possíveis anomalias nos dados. Este processo não apenas ajuda a identificar padrões relevantes, mas também fornece uma base sólida para a seleção de variáveis e construção de modelos preditivos. Ao explorar os dados, é possível descobrir relações implícitas entre as variáveis e verificar se os dados disponíveis são suficientes e adequados para atingir os objetivos do estudo.
Ter uma consciência situacional dos dados permite identificar outliers, valores faltantes e distribuições inesperadas que podem impactar negativamente a modelagem. Por exemplo, a identificação de uma variável com alta variância ou multicolinearidade é fundamental para evitar problemas como a instabilidade do modelo. Além disso, a EDA auxilia na escolha de transformações apropriadas para as variáveis, ajustando os dados para atender aos pressupostos do modelo. Este passo inicial é crucial para garantir a validade e a confiabilidade das análises subsequentes, além de direcionar melhor os esforços do projeto.
def visaogeral(df, messagem):
print(f'{messagem}:\n')
print("Qtd Observações:", df.shape[0])
print("\nQtd Atributos:", df.shape[1])
print("\nAtributos:")
print(df.columns.tolist())
print("\nQtd Valores missing:", df.isnull().sum().values.sum())
print("\nValores Unicos: indicativo de valores categóricos")
print(df.nunique().sort_values(ascending=True).head(40))
visaogeral(data,'Visão Geral dataSet treino')
Visão Geral dataSet treino: Qtd Observações: 2930 Qtd Atributos: 82 Atributos: ['Order', 'PID', 'MS SubClass', 'MS Zoning', 'Lot Frontage', 'Lot Area', 'Street', 'Alley', 'Lot Shape', 'Land Contour', 'Utilities', 'Lot Config', 'Land Slope', 'Neighborhood', 'Condition 1', 'Condition 2', 'Bldg Type', 'House Style', 'Overall Qual', 'Overall Cond', 'Year Built', 'Year Remod/Add', 'Roof Style', 'Roof Matl', 'Exterior 1st', 'Exterior 2nd', 'Mas Vnr Type', 'Mas Vnr Area', 'Exter Qual', 'Exter Cond', 'Foundation', 'Bsmt Qual', 'Bsmt Cond', 'Bsmt Exposure', 'BsmtFin Type 1', 'BsmtFin SF 1', 'BsmtFin Type 2', 'BsmtFin SF 2', 'Bsmt Unf SF', 'Total Bsmt SF', 'Heating', 'Heating QC', 'Central Air', 'Electrical', '1st Flr SF', '2nd Flr SF', 'Low Qual Fin SF', 'Gr Liv Area', 'Bsmt Full Bath', 'Bsmt Half Bath', 'Full Bath', 'Half Bath', 'Bedroom AbvGr', 'Kitchen AbvGr', 'Kitchen Qual', 'TotRms AbvGrd', 'Functional', 'Fireplaces', 'Fireplace Qu', 'Garage Type', 'Garage Yr Blt', 'Garage Finish', 'Garage Cars', 'Garage Area', 'Garage Qual', 'Garage Cond', 'Paved Drive', 'Wood Deck SF', 'Open Porch SF', 'Enclosed Porch', '3Ssn Porch', 'Screen Porch', 'Pool Area', 'Pool QC', 'Fence', 'Misc Feature', 'Misc Val', 'Mo Sold', 'Yr Sold', 'Sale Type', 'Sale Condition', 'SalePrice'] Qtd Valores missing: 15749 Valores Unicos: indicativo de valores categóricos Street 2 Alley 2 Central Air 2 Land Slope 3 Bsmt Half Bath 3 Half Bath 3 Garage Finish 3 Utilities 3 Paved Drive 3 Lot Shape 4 Bsmt Exposure 4 Kitchen AbvGr 4 Mas Vnr Type 4 Land Contour 4 Exter Qual 4 Bsmt Full Bath 4 Pool QC 4 Fence 4 Heating QC 5 Electrical 5 Bsmt Cond 5 Bldg Type 5 Fireplace Qu 5 Kitchen Qual 5 Lot Config 5 Bsmt Qual 5 Misc Feature 5 Yr Sold 5 Garage Qual 5 Full Bath 5 Fireplaces 5 Exter Cond 5 Garage Cond 5 Garage Cars 6 Heating 6 BsmtFin Type 1 6 Roof Style 6 Foundation 6 Garage Type 6 BsmtFin Type 2 6 dtype: int64
O conjunto de dados utilizado contém 2930 observações e 82 atributos, representando uma ampla gama de características das propriedades imobiliárias em Ames, Iowa. Entre essas colunas, foram identificados 15.749 valores faltantes, o que demanda atenção no tratamento durante a preparação dos dados para evitar prejuízos à qualidade do modelo. Adicionalmente, algumas variáveis possuem poucos valores únicos, como Street, Alley e Central Air, que indicam a possibilidade de serem categóricas. A análise inicial das características permite uma melhor compreensão estrutural dos dados, fornecendo insights sobre possíveis desafios, como o tratamento de dados ausentes e a manipulação de variáveis categóricas, fundamentais para a construção de um modelo robusto e confiável. Essa visão geral é essencial para definir as estratégias adequadas nas etapas subsequentes de preparação e análise dos dados.
data.columns
Index(['Order', 'PID', 'MS SubClass', 'MS Zoning', 'Lot Frontage', 'Lot Area',
'Street', 'Alley', 'Lot Shape', 'Land Contour', 'Utilities',
'Lot Config', 'Land Slope', 'Neighborhood', 'Condition 1',
'Condition 2', 'Bldg Type', 'House Style', 'Overall Qual',
'Overall Cond', 'Year Built', 'Year Remod/Add', 'Roof Style',
'Roof Matl', 'Exterior 1st', 'Exterior 2nd', 'Mas Vnr Type',
'Mas Vnr Area', 'Exter Qual', 'Exter Cond', 'Foundation', 'Bsmt Qual',
'Bsmt Cond', 'Bsmt Exposure', 'BsmtFin Type 1', 'BsmtFin SF 1',
'BsmtFin Type 2', 'BsmtFin SF 2', 'Bsmt Unf SF', 'Total Bsmt SF',
'Heating', 'Heating QC', 'Central Air', 'Electrical', '1st Flr SF',
'2nd Flr SF', 'Low Qual Fin SF', 'Gr Liv Area', 'Bsmt Full Bath',
'Bsmt Half Bath', 'Full Bath', 'Half Bath', 'Bedroom AbvGr',
'Kitchen AbvGr', 'Kitchen Qual', 'TotRms AbvGrd', 'Functional',
'Fireplaces', 'Fireplace Qu', 'Garage Type', 'Garage Yr Blt',
'Garage Finish', 'Garage Cars', 'Garage Area', 'Garage Qual',
'Garage Cond', 'Paved Drive', 'Wood Deck SF', 'Open Porch SF',
'Enclosed Porch', '3Ssn Porch', 'Screen Porch', 'Pool Area', 'Pool QC',
'Fence', 'Misc Feature', 'Misc Val', 'Mo Sold', 'Yr Sold', 'Sale Type',
'Sale Condition', 'SalePrice'],
dtype='object')
Para construir o modelo de regressão linear, foi realizada uma seleção das variáveis explicativas com base em sua possível relevância teórica e correlação com a variável dependente SalePrice (preço de venda). A seleção teve como objetivo identificar características imobiliárias que pudessem fornecer maior poder preditivo, além de garantir a interpretabilidade do modelo. As 14 variáveis escolhidas representam diferentes aspectos das propriedades, desde características estruturais até atributos qualitativos.
Variáveis Selecionadas
GrLivArea: Área habitável acima do solo (em pés quadrados). Representa o espaço funcional disponível na casa.
TotalBsmtSF: Área total do porão (em pés quadrados). Reflete o tamanho adicional utilizável na propriedade.
LotArea: Área total do terreno (em pés quadrados). Indica o espaço externo disponível.
Fireplaces: Número de lareiras. Representa conforto adicional e valorização estética.
WoodDeckSF: Área do deck de madeira (em pés quadrados). Indica melhorias na área externa.
BedroomAbvGr: Número de quartos acima do solo. Reflete a capacidade funcional da casa para acomodação.
TotRmsAbvGrd: Número total de cômodos acima do solo. Representa a dimensão geral da casa.
HouseAge: Idade da casa, calculada como 2024 - Ano de Construção. Representa o tempo desde a construção.
FullBath: Número de banheiros completos acima do solo. Reflete a funcionalidade adicional da casa.
OverallQual: Avaliação geral da qualidade da casa (escala de 1 a 10). Mede o padrão construtivo e acabamentos.
OverallCond: Condição geral da casa (escala de 1 a 10). Reflete o estado de conservação.
KitchenQual: Qualidade da cozinha (categorias: Excelente, Boa, Regular, Pobre). Representa um fator estético importante.
GarageCars: Capacidade da garagem (número de carros). Indica conveniência adicional.
BldgType: Tipo de construção (ex.: residencial unifamiliar, duplex). Representa o tipo de ocupação do imóvel.
Essas variáveis foram escolhidas devido à sua relevância prática e potencial impacto no preço de venda das propriedades.
Criou-se também. com base nas features de data uma varíavel de idade que a casa possui, tomando como base o ano de 2024!
# Criar nova variável HouseAge
data["HouseAge"] = 2024 - data["Year Built"]
selected_features = [
"Gr Liv Area", "Garage Cars", "Total Bsmt SF", "Lot Area", "Overall Qual",
"Kitchen Qual", "Overall Cond", "Fireplaces", "Wood Deck SF", "Bedroom AbvGr", "TotRms AbvGrd", "HouseAge",
"Full Bath", "Bldg Type"
]
X = data[selected_features]
y = data["SalePrice"]
def missing_values_table(df):
mis_val = df.isnull().sum()
mis_val_percent = 100 * df.isnull().sum() / len(df)
mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)
mis_val_table_ren_columns = mis_val_table.rename(
columns = {0 : 'Missing Values', 1 : '% of Total Values'})
mis_val_table_ren_columns = mis_val_table_ren_columns[
mis_val_table_ren_columns.iloc[:,1] != 0].sort_values(
'% of Total Values', ascending=False).round(1)
print ("Seu dataframe tem " + str(df.shape[1]) + " colunas.\n"
"Há " + str(mis_val_table_ren_columns.shape[0]) +
" colunas que possuem valores ausentes.")
return mis_val_table_ren_columns
y.isnull().sum()
np.int64(0)
A varíavel dependente não possui nenhum valor missing!
missing_values_table(X)
Seu dataframe tem 14 colunas. Há 2 colunas que possuem valores ausentes.
| Missing Values | % of Total Values | |
|---|---|---|
| Garage Cars | 1 | 0.0 |
| Total Bsmt SF | 1 | 0.0 |
Das 14 variáveis selecionadas para explicar a variável dependente SalePrice, algumas apresentam valores ausentes. O tratamento de dados faltantes é uma etapa essencial, pois a maioria dos modelos de aprendizado de máquina é sensível a valores nulos ou incompletos. Este tratamento pode envolver técnicas como imputação de valores, remoção de registros ou substituição por medidas estatísticas.
No entanto, no presente caso, o número de valores ausentes é pequeno e restrito a poucos registros. Por isso, optamos por uma abordagem direta: excluir os registros com dados faltantes. Essa decisão simplifica o processo e reduz o impacto potencial de estimativas inadequadas, garantindo que os dados restantes estejam completos e prontos para a modelagem. Esta escolha é apropriada, considerando o objetivo do estudo e a quantidade limitada de valores ausentes.
X = X.dropna()
y = y[X.index]
y.describe()
count 2928.000000 mean 180841.033811 std 79889.904415 min 12789.000000 25% 129500.000000 50% 160000.000000 75% 213500.000000 max 755000.000000 Name: SalePrice, dtype: float64
A variável dependente SalePrice representa o preço de venda das propriedades e é a principal métrica a ser modelada e explicada. Com base no resumo estatístico, tem-se:
Média (mean): O preço médio das propriedades é de aproximadamente $180.796, refletindo o valor típico de venda na região de Ames, Iowa.
Desvio Padrão (std): $79.886, indicando uma alta variabilidade nos preços, com algumas propriedades significativamente mais caras ou mais baratas que a média.
Valores Mínimo e Máximo (min e max): O menor preço registrado foi de $12.789, enquanto o maior chegou a $755.000, mostrando uma grande amplitude nos valores das propriedades.
Quartis (25%, 50% e 75%):
25% (primeiro quartil): 25% das propriedades têm preços abaixo de $129.500.
50% (mediana): O preço mediano é $160.000, indicando que metade das propriedades custa mais e metade custa menos.
75% (terceiro quartil): 25% das propriedades mais caras têm preços acima de $213.500.
Esses dados mostram que os preços de venda têm uma distribuição assimétrica e variam amplamente, refletindo diferenças significativas nas características das propriedades. Essa variabilidade será explorada durante a modelagem para identificar quais fatores influenciam mais fortemente os preços.
y.quantile([0.80,0.96,0.97])
0.80 230000.00 0.96 354920.00 0.97 377440.06 Name: SalePrice, dtype: float64
Esses percentis acima, indicam que 97% das propriedades estão distribuídas entre o valor mínimo de $12.789 e $377.435, com apenas 3% das propriedades ultrapassando este limite. Essa distribuição reflete que a maior parte das propriedades está concentrada em faixas de preço mais acessíveis, enquanto os valores mais altos representam propriedades de luxo ou com características muito diferenciadas.
Esses dados sugere que os preços de venda têm uma distribuição assimétrica e variam amplamente, refletindo diferenças significativas nas características das propriedades.
plt.figure(figsize=(10, 6))
plt.plot(np.sort(y), label="SalePrice", color='purple')
plt.title("Amplitude de SalePrice")
plt.xlabel("Índice Ordenado")
plt.ylabel("Preço de Venda")
plt.legend()
plt.show()
Ordenando a variável SalePrice observa-se sua amplitude, destacando uma curva crescente acentuada para as propriedades de maior valor. A maior parte dos preços está concentrada em faixas moderadas, enquanto os valores mais altos representam outliers ou propriedades de luxo. Essa visualização ajuda a identificar a assimetria e a variabilidade dos dados, elementos que influenciarão diretamente as etapas de modelagem e análise.
plt.figure(figsize=(10, 6))
sns.boxplot(y=y, color='cyan')
plt.title("Boxplot de SalePrice")
plt.xlabel("SalePrice")
plt.show()
O boxplot da variável SalePrice fornece informações importantes sobre a distribuição dos preços de venda. A mediana está localizada dentro da faixa interquartílica relativamente estreita, indicando que a maior parte dos preços está concentrada em torno de valores moderados. O gráfico destaca a presença de diversos outliers acima do limite superior, representando propriedades com preços extremamente altos. Esses outliers podem ter impacto significativo na modelagem e devem ser considerados no processo de análise, especialmente na validação dos pressupostos estatísticos.
# Gráfico de QQ-Plot para verificar normalidade
plt.figure(figsize=(10, 6))
sm.qqplot(y, line='s', fit=True)
plt.title("QQ-Plot de SalePrice")
plt.show()
<Figure size 1000x600 with 0 Axes>
O QQ-Plot da variável SalePrice avalia a aderência dos dados à normalidade. Observa-se que, embora os dados centrais estejam próximos da linha de referência, os extremos (valores mais baixos e mais altos) desviam significativamente, indicando caudas longas. Esse padrão sugere que a variável não segue uma distribuição normal perfeita, o que pode impactar análises que assumem normalidade. Transformações, como o logaritmo, podem ser consideradas para corrigir essa característica, se necessário para a modelagem.
# Estatísticas descritivas adicionais
print("Skewness (Assimetria):", skew(y))
print("Kurtosis (Curtose):", kurtosis(y))
Skewness (Assimetria): 1.7426236420109267 Kurtosis (Curtose): 5.107524847568088
A análise da assimetria (1,743) e da curtose (5,108) reforça as observações do QQ-Plot. A assimetria positiva indica uma distribuição com cauda longa à direita, causada por propriedades com preços muito elevados. Já a curtose elevada reflete caudas mais pesadas do que a normalidade, indicando a presença de outliers. Esses fatores sugerem a possibilidade de transformações para ajustar a variável SalePrice e melhorar a adequação dos modelos estatísticos.
plt.figure(figsize=(10, 6))
sns.histplot(y, kde=True, bins=30, color='blue')
plt.title("Histograma de SalePrice")
plt.xlabel("Preço de Venda")
plt.ylabel("Frequência")
plt.show()
O histograma da variável SalePrice mostra uma distribuição assimétrica à direita, confirmando a presença de propriedades com preços significativamente mais altos que a maioria. A maioria das observações está concentrada na faixa de $100.000 a $200.000. Se assimetria dos dados for sensível ao modelo de ML é um indício claro que deverá considerar transformações para corrigir a serem feitas antes da modelagem.
X.head()
| Gr Liv Area | Garage Cars | Total Bsmt SF | Lot Area | Overall Qual | Kitchen Qual | Overall Cond | Fireplaces | Wood Deck SF | Bedroom AbvGr | TotRms AbvGrd | HouseAge | Full Bath | Bldg Type | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1656 | 2.0 | 1080.0 | 31770 | 6 | TA | 5 | 2 | 210 | 3 | 7 | 64 | 1 | 1Fam |
| 1 | 896 | 1.0 | 882.0 | 11622 | 5 | TA | 6 | 0 | 140 | 2 | 5 | 63 | 1 | 1Fam |
| 2 | 1329 | 1.0 | 1329.0 | 14267 | 6 | Gd | 6 | 0 | 393 | 3 | 6 | 66 | 1 | 1Fam |
| 3 | 2110 | 2.0 | 2110.0 | 11160 | 7 | Ex | 5 | 2 | 0 | 3 | 8 | 56 | 2 | 1Fam |
| 4 | 1629 | 2.0 | 928.0 | 13830 | 5 | TA | 5 | 1 | 212 | 3 | 6 | 27 | 2 | 1Fam |
As variáveis explicativas selecionadas foram analisadas individualmente para entender a relação entre cada uma delas e a variável dependente SalePrice. Essa análise ajuda a identificar padrões importantes e avaliar a força das associações.
for feature in selected_features:
plt.figure(figsize=(10, 6))
sns.lineplot(x=X[feature], y=y, palette="viridis")
plt.title(f"Relação entre {feature} e SalePrice")
plt.xlabel(feature)
plt.ylabel("SalePrice")
plt.show()
Podemos realizar algumas considerações e com base no comportamento das preditoras com a variável alvo ter algumas compreensões, como:
A variável HouseAge representa a idade da propriedade, calculada a partir do ano de construção. Essa variável é comumente associada à depreciação do imóvel, especialmente para construções mais antigas. Pode-se observar que o gráfico revela uma relação inversa com o preço de venda: imóveis mais antigos tendem a ter preços mais baixos, enquanto imóveis mais recentes mantêm valores mais elevados.
Para a variável Fireplaces que reflete o número de lareiras presentes na propriedade. Este elemento é frequentemente associado ao conforto e à sofisticação estética do imóvel. Sugere uma relação positiva entre o número de lareiras e o preço de venda. Propriedades com uma ou duas lareiras mostram um aumento expressivo nos preços. Contudo, o impacto adicional diminui a partir de três lareiras, possivelmente devido a limitações práticas ou menor representatividade de imóveis com um número maior de lareiras nos dados.
OverallQual avalia a qualidade geral do material e do acabamento da propriedade, em uma escala de 1 a 10. A relação observada é linear e positiva. Nota-se uma tendência clara de aumento no preço de venda à medida que a qualidade geral melhora. Propriedades com alta qualidade (valores 9 e 10) apresentam os preços mais elevados, indicando que essa característica pode exercer influência no preço final.
Uma outra variável que podemos tecer uma avaliação é a KitchenQual que avalia a qualidade da cozinha em categorias, como Excelente (Ex), Boa (Gd), Típica/Adequada (TA), e Fraca (Fa). A relação com SalePrice é claramente positiva, especialmente em categorias de qualidade superior. Sendo assim, propriedades com cozinhas de qualidade "Excelente" apresentam os maiores preços médios, enquanto aquelas classificadas como "Fraca" têm preços significativamente menores. Essa diferença destaca a direção do impacto que a qualidade da cozinha pode ter na valorização da propriedade.
X.info()
<class 'pandas.core.frame.DataFrame'> Index: 2928 entries, 0 to 2929 Data columns (total 14 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Gr Liv Area 2928 non-null int64 1 Garage Cars 2928 non-null float64 2 Total Bsmt SF 2928 non-null float64 3 Lot Area 2928 non-null int64 4 Overall Qual 2928 non-null int64 5 Kitchen Qual 2928 non-null object 6 Overall Cond 2928 non-null int64 7 Fireplaces 2928 non-null int64 8 Wood Deck SF 2928 non-null int64 9 Bedroom AbvGr 2928 non-null int64 10 TotRms AbvGrd 2928 non-null int64 11 HouseAge 2928 non-null int64 12 Full Bath 2928 non-null int64 13 Bldg Type 2928 non-null object dtypes: float64(2), int64(10), object(2) memory usage: 343.1+ KB
numerical_features = [
"Gr Liv Area", "Garage Cars", "Total Bsmt SF", "Lot Area", "Fireplaces",
"Wood Deck SF", "Bedroom AbvGr", "TotRms AbvGrd", "HouseAge", "Full Bath"
]
Os gráficos gerados com a combinação de scatterplot e regplot apresentam, simultaneamente, os dados de dispersão e a linha de regressão linear para cada variável numérica selecionada. Permitem visualizar as relações entre as variáveis explanatórias e a variável dependente SalePrice. A dispersão dos pontos fornece insights sobre a variação dos preços de venda em função de cada característica, enquanto a linha de regressão destaca a tendência geral da relação. Essa abordagem facilita a identificação de padrões, possíveis associações lineares, outliers e comportamentos não lineares que podem impactar a modelagem.
for feature in numerical_features:
plt.figure(figsize=(10, 6))
sns.scatterplot(x=X[feature], y=y, color='orange', label='Dados de dispersão')
sns.regplot(x=X[feature], y=y, scatter=False, color='blue', label='Regressão Linear')
plt.title(f"Relação entre {feature} e SalePrice")
plt.xlabel(feature)
plt.ylabel("SalePrice")
plt.legend()
plt.show()
X[numerical_features].corr()
| Gr Liv Area | Garage Cars | Total Bsmt SF | Lot Area | Fireplaces | Wood Deck SF | Bedroom AbvGr | TotRms AbvGrd | HouseAge | Full Bath | |
|---|---|---|---|---|---|---|---|---|---|---|
| Gr Liv Area | 1.000000 | 0.488621 | 0.444819 | 0.285517 | 0.455029 | 0.249830 | 0.516607 | 0.807800 | -0.241949 | 0.630107 |
| Garage Cars | 0.488621 | 1.000000 | 0.437608 | 0.179368 | 0.320990 | 0.241035 | 0.091036 | 0.355230 | -0.537312 | 0.477997 |
| Total Bsmt SF | 0.444819 | 0.437608 | 1.000000 | 0.253577 | 0.333007 | 0.230049 | 0.051969 | 0.280721 | -0.407479 | 0.325135 |
| Lot Area | 0.285517 | 0.179368 | 0.253577 | 1.000000 | 0.256865 | 0.157141 | 0.136421 | 0.216403 | -0.023044 | 0.127326 |
| Fireplaces | 0.455029 | 0.320990 | 0.333007 | 0.256865 | 1.000000 | 0.228134 | 0.076737 | 0.302503 | -0.170046 | 0.229850 |
| Wood Deck SF | 0.249830 | 0.241035 | 0.230049 | 0.157141 | 0.228134 | 1.000000 | 0.029422 | 0.154494 | -0.229263 | 0.179224 |
| Bedroom AbvGr | 0.516607 | 0.091036 | 0.051969 | 0.136421 | 0.076737 | 0.029422 | 1.000000 | 0.672529 | 0.055334 | 0.359251 |
| TotRms AbvGrd | 0.807800 | 0.355230 | 0.280721 | 0.216403 | 0.302503 | 0.154494 | 0.672529 | 1.000000 | -0.111429 | 0.528506 |
| HouseAge | -0.241949 | -0.537312 | -0.407479 | -0.023044 | -0.170046 | -0.229263 | 0.055334 | -0.111429 | 1.000000 | -0.469936 |
| Full Bath | 0.630107 | 0.477997 | 0.325135 | 0.127326 | 0.229850 | 0.179224 | 0.359251 | 0.528506 | -0.469936 | 1.000000 |
plt.figure(figsize=(12, 8))
correlation_matrix = X[numerical_features].corr()
sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm", fmt=".2f")
plt.title("Matriz de Correlação - Variáveis Numéricas")
plt.show()
A matriz de correlação permite identificar a relação linear entre variáveis numéricas. Nesse contexto, cada valor da matriz, variando entre -1 e 1, indica a força e a direção do relacionamento entre duas variáveis. Valores próximos de 1 representam uma correlação positiva forte, enquanto valores próximos de -1 indicam uma correlação negativa forte. Já valores próximos de 0 sugerem ausência de relação linear significativa. (Silva, 2023)
No gráfico, as cores facilitam a interpretação visual: tons avermelhados indicam correlação positiva, enquanto tons azulados representam correlação negativa. Por exemplo, observa-se uma forte correlação positiva entre Gr Liv Area e TotRms Abv Grd (0.81), indicando que, em geral, propriedades com maior área habitável acima do solo tendem a ter mais cômodos. Por outro lado, variáveis como HouseAge apresentam correlações negativas moderadas com outras variáveis, como Garage Cars (-0.54), sugerindo que casas mais antigas tendem a ter garagens menores. Essa análise permite identificar variáveis altamente correlacionadas, que podem influenciar a multicolinearidade nos modelos de regressão.
3.1.4.2.4 Avaliando a Multicolinearidade ¶
A avaliação de multicolinearidade é um passo essencial em análises de regressão linear, pois a presença de correlações elevadas entre variáveis explicativas pode distorcer os coeficientes do modelo, dificultando a interpretação e reduzindo sua precisão preditiva. Uma das ferramentas mais utilizadas para diagnosticar multicolinearidade é o Fator de Inflação da Variância (Variance Inflation Factor - VIF). O VIF mede o quanto a variância de um coeficiente de regressão é inflada devido à correlação entre variáveis explicativas. (Gujarati, 2009)
Vlores de VIF acima de 10 são geralmente considerados indicadores de multicolinearidade severa, enquanto valores próximos de 1 sugerem baixa correlação. Essa métrica ajuda a identificar quais variáveis podem ser redundantes e devem ser ajustadas ou removidas do modelo, melhorando sua robustez e interpretabilidade.
vif_data = pd.DataFrame()
vif_data["Feature"] = numerical_features
vif_data["VIF"] = [variance_inflation_factor(X[numerical_features].values, i) for i in range(X[numerical_features].shape[1])]
print("\nVariance Inflation Factor (VIF):")
print(vif_data)
Variance Inflation Factor (VIF):
Feature VIF
0 Gr Liv Area 40.391979
1 Garage Cars 10.312104
2 Total Bsmt SF 8.848557
3 Lot Area 3.078425
4 Fireplaces 2.575616
5 Wood Deck SF 1.751656
6 Bedroom AbvGr 25.504382
7 TotRms AbvGrd 64.253768
8 HouseAge 4.314102
9 Full Bath 16.892883
"Em geral, considera-se um problema VIF > 5. Mas esta é uma regra de bolso. Há quem diga que acima de 10 é que se deve corrigir o problema de colinearidade... Algumas alternativas para solucionar problemas de multicolinearidade são: regressão por mínimos quadrados parciais (partial least squares, do inglês), regressão de componentes principais (similar a última), regressão de cumeeira (ridge regression)."
(Silva, 2023, p. 199)
Um dos pressupostos fundamentais da regressão linear, que é a ausência de multicolinearidade entre as variáveis independentes, foi claramente violado, conforme evidenciado pelos valores do VIF. Variáveis como Gr Liv Area (VIF = 40.39), TotRms AbvGrd (VIF = 64.25) e Bedroom AbvGr (VIF = 25.50) indicam níveis de multicolinearidade. Essa condição compromete a estabilidade e a interpretabilidade do modelo, podendo inflacionar os erros padrão dos coeficientes e dificultar a identificação da real contribuição de cada variável na previsão.
No entanto, usaremos a "Licença científica" e seguiremos em frente para explorar como o modelo se comporta, reconhecendo que, conforme o ciclo CRISP-DM, a transição entre as etapas de preparação dos dados e modelagem pode ser feita iterativamente. Isso permite revisitar as etapas, ajustar o tratamento de multicolinearidade e refinar o modelo conforme necessário, garantindo maior robustez e adequação aos dados ao longo do processo.
3.1.4.3 Explanatórias Categóricas ¶
Essa etapa dá continuidade à análise das variáveis explicativas, focando nos dados categóricos. Utilizamos o boxplot como ferramenta principal para visualizar a distribuição da variável resposta em cada categoria, o que permite identificar diferenças significativas entre grupos, detectar outliers e avaliar tendências gerais. Esses insights ajudam a determinar se as categorias possuem poder explicativo relevante para o modelo, guiando ajustes e decisões na preparação dos dados.
categorical_features = ["Overall Qual", "Kitchen Qual", "Overall Cond", "Bldg Type"]
for feature in categorical_features:
plt.figure(figsize=(10, 6))
sns.boxplot(x=data[feature], y=y, palette="viridis")
plt.title(f"Relação entre {feature} e SalePrice")
plt.xlabel(feature)
plt.ylabel("SalePrice")
plt.show()
4.1 Feature Engineer ¶
Após a Análise Exploratória dos Dados (EDA), iniciamos a etapa de pré-processamento, essencial para preparar os dados de forma adequada para a modelagem.
Nesse trabalho, (i) transformamos variáveis categóricas em variáveis dummy, permitindo que classes representadas como strings sejam convertidas em um formato numérico compreensível para os algoritmos de aprendizado. Além disso, (ii) tratamos os valores ausentes, optando por remover observações com dados faltantes, dado seu impacto mínimo (apenas 2 registros).
Essas ações visam garantir que os dados estejam limpos, estruturados e prontos para alimentar o modelo, maximizando sua eficácia e desempenho.
X
| Gr Liv Area | Garage Cars | Total Bsmt SF | Lot Area | Overall Qual | Kitchen Qual | Overall Cond | Fireplaces | Wood Deck SF | Bedroom AbvGr | TotRms AbvGrd | HouseAge | Full Bath | Bldg Type | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1656 | 2.0 | 1080.0 | 31770 | 6 | TA | 5 | 2 | 210 | 3 | 7 | 64 | 1 | 1Fam |
| 1 | 896 | 1.0 | 882.0 | 11622 | 5 | TA | 6 | 0 | 140 | 2 | 5 | 63 | 1 | 1Fam |
| 2 | 1329 | 1.0 | 1329.0 | 14267 | 6 | Gd | 6 | 0 | 393 | 3 | 6 | 66 | 1 | 1Fam |
| 3 | 2110 | 2.0 | 2110.0 | 11160 | 7 | Ex | 5 | 2 | 0 | 3 | 8 | 56 | 2 | 1Fam |
| 4 | 1629 | 2.0 | 928.0 | 13830 | 5 | TA | 5 | 1 | 212 | 3 | 6 | 27 | 2 | 1Fam |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2925 | 1003 | 2.0 | 1003.0 | 7937 | 6 | TA | 6 | 0 | 120 | 3 | 6 | 40 | 1 | 1Fam |
| 2926 | 902 | 2.0 | 864.0 | 8885 | 5 | TA | 5 | 0 | 164 | 2 | 5 | 41 | 1 | 1Fam |
| 2927 | 970 | 0.0 | 912.0 | 10441 | 5 | TA | 5 | 0 | 80 | 3 | 6 | 32 | 1 | 1Fam |
| 2928 | 1389 | 2.0 | 1389.0 | 10010 | 5 | TA | 5 | 1 | 240 | 2 | 6 | 50 | 1 | 1Fam |
| 2929 | 2000 | 3.0 | 996.0 | 9627 | 7 | TA | 5 | 1 | 190 | 3 | 9 | 31 | 2 | 1Fam |
2928 rows × 14 columns
categorical_features_dummies = ['Kitchen Qual','Bldg Type']
X = pd.get_dummies(X, columns=categorical_features_dummies, drop_first=True)
X
| Gr Liv Area | Garage Cars | Total Bsmt SF | Lot Area | Overall Qual | Overall Cond | Fireplaces | Wood Deck SF | Bedroom AbvGr | TotRms AbvGrd | HouseAge | Full Bath | Kitchen Qual_Fa | Kitchen Qual_Gd | Kitchen Qual_Po | Kitchen Qual_TA | Bldg Type_2fmCon | Bldg Type_Duplex | Bldg Type_Twnhs | Bldg Type_TwnhsE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1656 | 2.0 | 1080.0 | 31770 | 6 | 5 | 2 | 210 | 3 | 7 | 64 | 1 | False | False | False | True | False | False | False | False |
| 1 | 896 | 1.0 | 882.0 | 11622 | 5 | 6 | 0 | 140 | 2 | 5 | 63 | 1 | False | False | False | True | False | False | False | False |
| 2 | 1329 | 1.0 | 1329.0 | 14267 | 6 | 6 | 0 | 393 | 3 | 6 | 66 | 1 | False | True | False | False | False | False | False | False |
| 3 | 2110 | 2.0 | 2110.0 | 11160 | 7 | 5 | 2 | 0 | 3 | 8 | 56 | 2 | False | False | False | False | False | False | False | False |
| 4 | 1629 | 2.0 | 928.0 | 13830 | 5 | 5 | 1 | 212 | 3 | 6 | 27 | 2 | False | False | False | True | False | False | False | False |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2925 | 1003 | 2.0 | 1003.0 | 7937 | 6 | 6 | 0 | 120 | 3 | 6 | 40 | 1 | False | False | False | True | False | False | False | False |
| 2926 | 902 | 2.0 | 864.0 | 8885 | 5 | 5 | 0 | 164 | 2 | 5 | 41 | 1 | False | False | False | True | False | False | False | False |
| 2927 | 970 | 0.0 | 912.0 | 10441 | 5 | 5 | 0 | 80 | 3 | 6 | 32 | 1 | False | False | False | True | False | False | False | False |
| 2928 | 1389 | 2.0 | 1389.0 | 10010 | 5 | 5 | 1 | 240 | 2 | 6 | 50 | 1 | False | False | False | True | False | False | False | False |
| 2929 | 2000 | 3.0 | 996.0 | 9627 | 7 | 5 | 1 | 190 | 3 | 9 | 31 | 2 | False | False | False | True | False | False | False | False |
2928 rows × 20 columns
# X = X.dropna()
# y = y[X.index]
4.2 Split dados ¶
Para avaliar o desempenho do modelo, é fundamental dividir os dados em conjuntos de treino e teste. Duas abordagens amplamente utilizadas são:
- (i) o método estático, implementado pela função train_test_split da biblioteca sklearn.model_selection, que separa os dados em uma única iteração; e
- (ii) a validação cruzada (Cross-validation), que realiza divisões aleatórias e avalia o modelo em diferentes subconjuntos para maior robustez.
Optamos pelo método estático, configurando 80% dos dados para treino e 20% para teste, garantindo simplicidade e uma divisão consistente para o desenvolvimento inicial do modelo.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
= output: dados pré-processados e splitados para iniciar a construção do modelo de ML
5. Seleção Algoritmos ¶
5.1 Algoritmos Regressores ¶
A regressão linear é uma técnica estatística utilizada para prever o valor de uma variável dependente (contínua) com base em uma ou mais variáveis independentes. O objetivo é estabelecer um modelo matemático que expresse a relação entre as variáveis, permitindo entender como determinadas variáveis explicativas influenciam a resposta. Um exemplo de seu uso é prever o preço de uma casa com base em seu tamanho, onde o preço é a variável dependente e o tamanho, a variável independente, ou seja, o objetivo do presente.
A abordagem baseia-se na suposição de que as variáveis estão linearmente relacionadas, permitindo que a relação seja descrita por uma equação linear simples ou múltipla. Para construir o modelo, é necessário treinar o algoritmo com dados históricos, identificar os padrões matemáticos subjacentes e, em seguida, usar esses padrões para fazer previsões. Essa simplicidade faz da regressão linear uma ferramenta amplamente utilizada em diversas áreas, como finanças, engenharia, e claro ciência de dados.
Além de sua facilidade de implementação, a regressão linear fornece coeficientes que são facilmente interpretáveis, permitindo compreender o impacto de cada variável independente na resposta. No entanto, sua aplicabilidade depende de atender a pressupostos importantes, como linearidade, homocedasticidade, independência dos erros e ausência de multicolinearidade.
Assume que os dados estão em Distribuição Normal e também assume que as variáveis são relevantes para a construção do modelo e que não sejam colineares, ou seja, variáveis com alta correlação (deve-se entregar ao algoritmo as variáveis realmente relevantes).
model = LinearRegression()
print(X.dtypes)
Gr Liv Area int64 Garage Cars float64 Total Bsmt SF float64 Lot Area int64 Overall Qual int64 Overall Cond int64 Fireplaces int64 Wood Deck SF int64 Bedroom AbvGr int64 TotRms AbvGrd int64 HouseAge int64 Full Bath int64 Kitchen Qual_Fa bool Kitchen Qual_Gd bool Kitchen Qual_Po bool Kitchen Qual_TA bool Bldg Type_2fmCon bool Bldg Type_Duplex bool Bldg Type_Twnhs bool Bldg Type_TwnhsE bool dtype: object
model.fit(X_train, y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
coefficients = pd.DataFrame({"Feature": X.columns, "Coefficient": model.coef_})
intercept = model.intercept_
y_pred_train = model.predict(X_train)
y_pred_test = model.predict(X_test)
residuals = y_test - y_pred_test
print("Coeficientes do modelo:")
print(coefficients)
Coeficientes do modelo:
Feature Coefficient
0 Gr Liv Area 5.284067e+01
1 Garage Cars 9.268205e+03
2 Total Bsmt SF 2.267557e+01
3 Lot Area 4.781547e-01
4 Overall Qual 1.386263e+04
5 Overall Cond 5.613652e+03
6 Fireplaces 6.895560e+03
7 Wood Deck SF 2.425044e+01
8 Bedroom AbvGr -7.058272e+03
9 TotRms AbvGrd 3.912949e+02
10 HouseAge -5.117012e+02
11 Full Bath -7.757054e+02
12 Kitchen Qual_Fa -4.978184e+04
13 Kitchen Qual_Gd -5.009302e+04
14 Kitchen Qual_Po 1.818989e-11
15 Kitchen Qual_TA -5.701537e+04
16 Bldg Type_2fmCon -5.484163e+03
17 Bldg Type_Duplex -1.590632e+04
18 Bldg Type_Twnhs -2.308489e+04
19 Bldg Type_TwnhsE -1.510283e+04
Coeficientes 𝛽 positivos indicam que, à medida que a variável explicativa associada aumenta (mantendo as outras constantes), o preço da variável dependente 𝑦 também aumenta. Ou seja, essas variáveis têm um impacto positivo no preço.
Coeficientes 𝛽 negativos indicam que, à medida que a variável explicativa associada aumenta, o preço (𝑦) diminui, tendo um impacto negativo no preço.
Essa relação é direta, e a magnitude do coeficiente representa o impacto médio da variável na resposta 𝑦. Por exemplo:
- Se 𝛽=50, um aumento de 1 unidade na variável 𝑥 correspondente resultará em um aumento médio de 50 unidades no preço (𝑦).
- Se 𝛽= −30, um aumento de 1 unidade em 𝑥 reduzirá, em média, o preço em 30 unidades.
Em termos práticos temos:
Gr Liv Area(52,84): A cada unidade adicional de área habitável, o valor predito aumenta em aproximadamente 52,84 unidades monetárias, mantendo as outras variáveis constantes.Garage Cars(9.268,21): Cada vaga adicional na garagem está associada a um aumento médio de 9.268,21 no valor predito.Overall Qual(13.862,63): Para cada ponto a mais na qualidade geral do imóvel, o valor predito aumenta em 13.862,63.Fireplaces(6.895,56): Cada lareira adicional está associada a um aumento médio de 6.895,56 no valor predito.Bedroom AbvGr(-7.058,27): Cada quarto adicional acima do térreo está associado a uma redução média de 7.058,27 no valor predito. Esse coeficiente pode parecer contraintuitivo e indicar multicolinearidade ou um padrão específico nos dados.HouseAge(-511,70): Cada ano adicional na idade da casa está associado a uma redução de 511,70 no valor predito, refletindo o impacto da depreciação.Kitchen Qual_Po(1.81e-11) é praticamente zero, indicando que esta categoria pode ser irrelevante ou ter poucos dados.
Portanto, o sinal do coeficiente + ou − indica a direção estatística da influência no modelo, enquanto o valor absoluto reflete a intensidade desse impacto. No entanto, é fundamental considerar as regras e o contexto do negócio ao interpretar os coeficientes, pois, embora o sinal seja estatisticamente relevante, a compreensão do problema e das variáveis no domínio aplicado é crucial para uma análise completa e adequada
5.2 Performance para Regressores ¶
Existem diversas métricas disponíveis para avaliar o desempenho de um modelo, cada uma com suas características e aplicações específicas. É considerado uma boa prática utilizar a mesma métrica ao comparar diferentes modelos, garantindo consistência e permitindo uma análise justa dos resultados. Para mais detalhes sobre as opções de métricas, consulte a documentação oficial do scikit-learn.
Métricas Para Avaliar Modelos de Regressão
- Mean Squared Error (MSE)
- Root Mean Squared Error (RMSE)
- Mean Absolute Error (MAE)
- R Squared (R²)
- Adjusted R Squared (R²)
- Mean Square Percentage Error (MSPE)
- Mean Absolute Percentage Error (MAPE)
- Root Mean Squared Logarithmic Error (RMSLE)
5.2.1 MSE ¶
O MSE é uma das métricas mais simples e amplamente utilizadas para avaliar o desempenho de modelos de regressão. Ele mede o erro quadrado médio entre as previsões do modelo e os valores reais da variável-alvo. Para cada ponto, calcula-se a diferença entre o valor predito e o valor observado, eleva-se ao quadrado, e, em seguida, calcula-se a média desses valores.
Um MSE maior indica um desempenho pior do modelo, enquanto um MSE de zero seria alcançado por um modelo perfeito. Essa métrica nunca assume valores negativos, pois os erros individuais são elevados ao quadrado, garantindo que todos sejam positivos. Apesar de sua simplicidade, o MSE pode ser influenciado por outliers, o que o torna menos útil em alguns cenários específicos.
train_rmse = np.sqrt(mean_squared_error(y_train, y_pred_train))
test_rmse = np.sqrt(mean_squared_error(y_test, y_pred_test))
# quanto menor melhor
print(f'O MSE do modelo é: {train_rmse} para os dados de treino e {test_rmse} para os dados de teste!')
O MSE do modelo é: 30689.400546900368 para os dados de treino e 37548.64604586386 para os dados de teste!
5.2.2 MAE ¶
O MAE é a média das diferenças absolutas entre as previsões do modelo e os valores reais da variável-alvo. Essa métrica fornece uma visão clara do quão distante, em média, as previsões estão dos valores reais, sem considerar a direção do erro (positiva ou negativa).
Um MAE igual a zero indica que o modelo não cometeu erros, ou seja, as previsões foram perfeitas. Por ser baseado em valores absolutos, o MAE é menos sensível a outliers em comparação com o MSE, o que pode torná-lo mais adequado em cenários onde grandes erros individuais não devem ter peso excessivo na avaliação do modelo.
train_mae = np.sqrt(mean_absolute_error(y_train, y_pred_train))
test_mae = np.sqrt(mean_absolute_error(y_test, y_pred_test))
# quanto menor melhor
print(f'O MAE do modelo é: {train_mae} para os dados de treino e {test_mae} para os dados de teste!')
O MAE do modelo é: 138.84418172919277 para os dados de treino e 144.42266773369224 para os dados de teste!
5.2.3 R² ¶
O R² é uma métrica amplamente utilizada para avaliar o quão bem o modelo explica a variabilidade dos dados observados. Ele mede a proporção da variância da variável-alvo que é explicada pelas variáveis independentes do modelo, oferecendo uma indicação do nível de precisão das previsões em relação aos valores observados.
Os valores do R² variam de 0 a 1, onde:
- 0 indica que o modelo não explica nenhuma variação nos dados (desempenho ruim).
- 1 representa um modelo perfeito, que explica 100% da variância da variável-alvo.
Embora o R² seja útil para interpretar a qualidade do ajuste do modelo, ele não avalia diretamente a magnitude dos erros, sendo necessário combiná-lo com outras métricas para uma análise mais completa.
train_r2 = r2_score(y_train, y_pred_train)
test_r2 = r2_score(y_test, y_pred_test)
print(f'O R2 do modelo é: {train_r2} para os dados de treino e {test_r2} para os dados de teste!')
O R2 do modelo é: 0.8408284871126857 para os dados de treino e 0.8285043729939088 para os dados de teste!
Consolidando as principais Técnicas de performance para Regressores¶
print("O MSE do modelo é:", train_rmse)
print("O MAE do modelo é:", train_mae)
print("O R² do modelo é:", train_r2)
O MSE do modelo é: 30689.400546900368 O MAE do modelo é: 138.84418172919277 O R² do modelo é: 0.8408284871126857
plt.figure(figsize=(10, 6))
sns.scatterplot(x=y_pred_test, y=residuals, color="blue")
plt.axhline(0, linestyle="--", color="red")
plt.title("Resíduos vs. Valores Preditos")
plt.xlabel("Valores Preditos")
plt.ylabel("Resíduos")
plt.show()
Os resíduos não estão uniformemente distribuídos ao longo da linha central (linha vermelha em zero). Existe um padrão de aumento na variância dos resíduos para valores preditos maiores, sugerindo que o modelo apresenta heterocedasticidade, ou seja, a variabilidade dos resíduos não é constante, fere pressupostos de uma regressão linear. Além de pontos distantes do centro, especialmente em valores preditos altos, indicam potenciais outliers ou casos que o modelo não conseguiu ajustar bem.
plt.figure(figsize=(10, 6))
sns.histplot(residuals, kde=True, color="purple")
plt.title("Distribuição dos Resíduos")
plt.xlabel("Resíduos")
plt.ylabel("Frequência")
plt.show()
O histograma indica que os resíduos estão concentrados em torno de zero, com uma leve assimetria. Embora o pico seja bem definido, as caudas mais alongadas sugerem que os resíduos não seguem uma distribuição perfeitamente normal. A curva roxa de densidade destaca a presença de uma cauda direita levemente mais longa, indicando que alguns resíduos positivos são maiores do que o esperado. Podemos inferir que a distribuição dos resíduos não é perfeitamente normal e pode influenciar a validade de inferências estatísticas, como os intervalos de confiança e testes de hipóteses.
sm.qqplot(residuals, line="s")
plt.title("QQ-Plot dos Resíduos")
plt.show()
Em um modelo ideal com resíduos normais, os pontos devem estar alinhados com a linha vermelha. Nos quantis centrais (em torno de zero), os resíduos seguem razoavelmente a linha de referência, indicando uma aproximação da normalidade para a maior parte dos dados. Muito embora, nos extremos, há desvios significativos da linha, com resíduos nas caudas (tanto inferiores quanto superiores) afastando-se da normalidade. Isso sugere a presença de outliers ou resíduos que não seguem bem a distribuição normal.
print("Média dos resíduos:", np.mean(residuals))
print("Desvio padrão dos resíduos:", np.std(residuals))
Média dos resíduos: 1820.1445778434927 Desvio padrão dos resíduos: 37504.504977313256
6. Conclusões ¶
O modelo de regressão linear ajustado apresentou um R² de 0,8, indicando que 80% da variabilidade do preço de venda das propriedades SalePrice pode ser explicada pelas variáveis explicativas selecionadas. Este resultado, à primeira vista, sugere uma boa capacidade preditiva. Contudo, é importante destacar que métricas de desempenho, por si só, não garantem a adequação estatística do modelo, especialmente quando os pressupostos fundamentais da regressão linear são violados.
Durante a etapa de análise exploratória de dados (EDA), identificamos indícios de fragilidade nos dados, como distribuições assimétricas, outliers e possível multicolinearidade entre as variáveis. Essas características foram confirmadas durante a avaliação dos resíduos e dos pressupostos do modelo. Os gráficos residuais indicaram a presença de padrões não aleatórios, heterocedasticidade e desvios significativos da normalidade, comprometendo a validade inferencial do modelo. Além disso, o cálculo do VIF revelou multicolinearidade em algumas variáveis, o que pode influenciar negativamente as estimativas dos coeficientes.
Com base no framework CRISP-DM, é evidente que o modelo deve retornar à fase de preparação e pré-processamento dos dados. Nesta etapa, será essencial adotar estratégias como transformações nas variáveis (ex.: logaritmo ou padronização), remoção ou tratamento de outliers, e redução de multicolinearidade, seja por meio de seleção de variáveis ou métodos de regularização, como Ridge ou Lasso.
Somente após um pré-processamento robusto, o modelo poderá ser reavaliado para garantir que atenda tanto aos pressupostos estatísticos quanto às métricas preditivas esperadas. Este ciclo de refinamento, conforme preconizado pelo CRISP-DM, é essencial para garantir um modelo confiável e interpretável, capaz de oferecer insights práticos e fundamentados sobre o impacto das características das propriedades no preço de venda.
GUJARATI, D. N., & Porter, D. C. (2009). Basic Econometrics (5th ed.). McGraw-Hill Education.
SILVA, Anderson Rodrigo da. Estatística decodificada. São Paulo: Editora Blucher, 2023. E-book. p.167. ISBN 9786555063585. Disponível em: https://unibb.minhabiblioteca.com.br/reader/books/9786555063585/. Acesso em: 15 dez. 2024.
SHEARER, C. (2000). The CRISP-DM Model: The New Blueprint for Data Mining. Journal of Data Warehousing, 5(4), 13–22.